Skip to contents

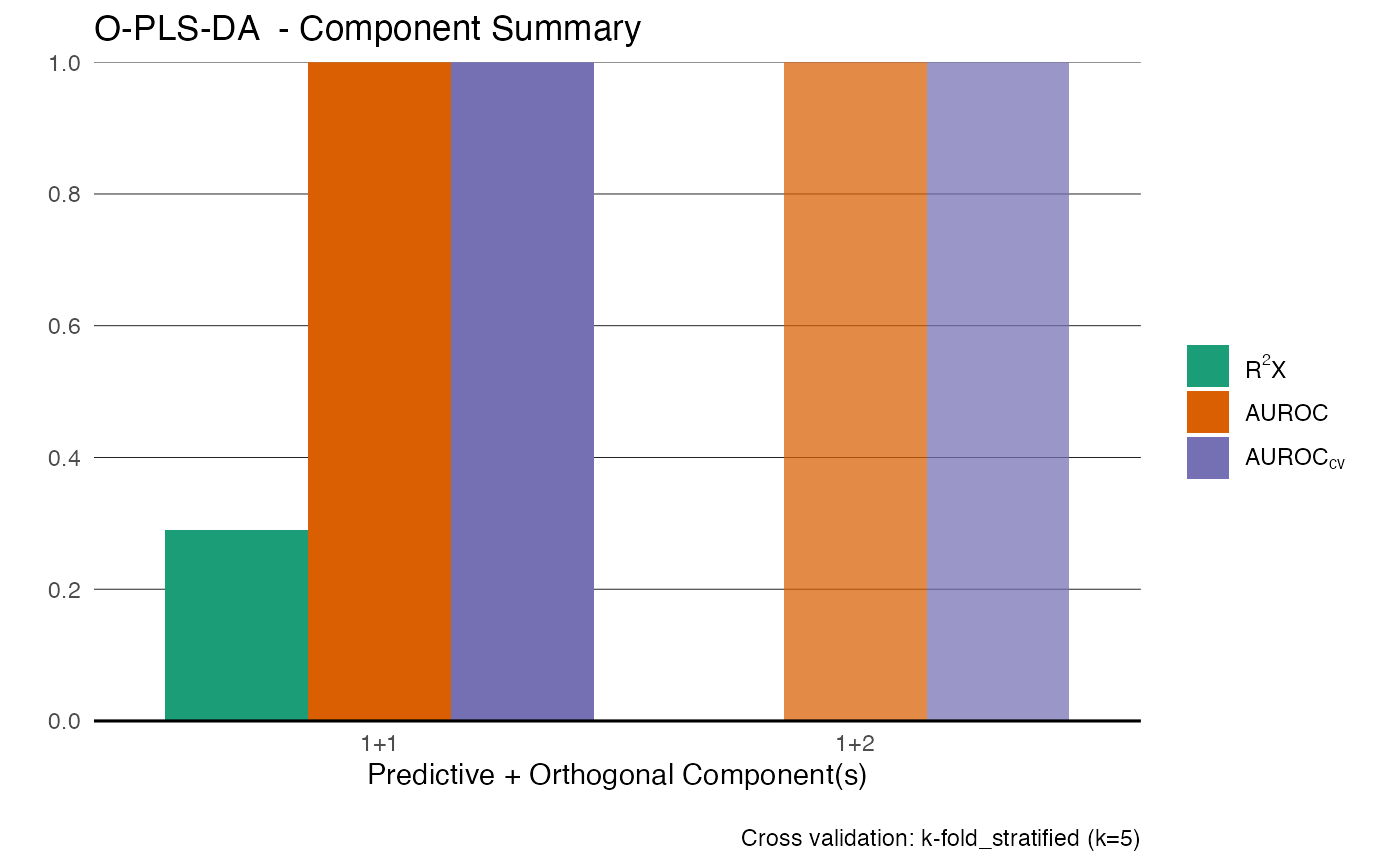
#' @title Orthogonal Partial Least Squares (O-PLS) #' #' @description #' Fits an Orthogonal Projections to Latent Structures (O-PLS) model for regression or classification. #' The number of orthogonal components is automatically selected using internal cross-validation. #' To avoid underfitting, components are added incrementally, while overfitting is prevented by requiring that each new component improves predictive performance beyond a defined threshold (ΔQ² / ΔAUROC > 0.05). This ensures the model captures relevant structure without modelling noise or irrelevant variation.

Source: R/opls.R
opls.Rd

#' @title Orthogonal Partial Least Squares (O-PLS) #' #' @description #' Fits an Orthogonal Projections to Latent Structures (O-PLS) model for regression or classification. #' The number of orthogonal components is automatically selected using internal cross-validation. #' To avoid underfitting, components are added incrementally, while overfitting is prevented by requiring that each new component improves predictive performance beyond a defined threshold (ΔQ² / ΔAUROC > 0.05). This ensures the model captures relevant structure without modelling noise or irrelevant variation.

Usage

opls(
  X,
  Y,
  center = TRUE,
  scale = "UV",
  cv = list(method = "k-fold_stratified", k = 7, split = 2/3),
  maxPCo = 5,
  plotting = TRUE
)

Arguments

X

Numeric matrix or data frame of predictors. Rows are samples; columns are features.

Y

Response variable. Vector or matrix. For classification, should be a factor or class labels; for regression, a numeric vector or matrix.

center

Logical. Should features be mean-centered? Default is TRUE.

scale

Character. Scaling method. Supported: "None", "UV" (unit variance), or "Pareto".

cv

Named list specifying cross-validation settings: method ("k-fold", "k-fold_stratified"), split (training set proportion), and k (number of folds).

maxPCo

Integer. Maximum number of orthogonal components to consider. Default is 5.

plotting

Logical. If TRUE, shows model summary plot.

Value

An S4 object of class OPLS_metabom8.

References

Trygg J, Wold S. (2002). Orthogonal projections to latent structures (O-PLS). Journal of Chemometrics, 16(3), 119–128.

Author

Torben Kimhofer

Examples

data("covid")
X <- covid$X
an <- covid$an

mod <- opls(X, an$type)
#> Performing discriminant analysis.
#> Reducing k to 5 due to small group size (min n = 5).
#> An O-PLS-DA model with 1 predictive and 1 orthogonal components was fitted.

summary(mod)
#>        Length         Class          Mode 
#>             1 OPLS_metabom8            S4